图像增强

来补课了，作为图像处理系列的第一篇，接下来会陆续更新相关知识，并附上对应的python代码，但是这里主要是不用一些现成的代码库，可能过程会有些麻烦不像python，但为了体会后面的原理，瑕不掩瑜，那就开始吧

在开始之前，先把整个代码需要的东西放在这里，后面再一个个放对应的模块

import PIL.Image as Image
import numpy as np
import cv2
import matplotlib.pyplot as plt
'''
因为要将PIL转换为numpy进行运算，所以这里写了个方便numpy显示结果的函数,(后面为了方便也没用，直接plt了)
'''
def show_img(image):
    image = Image.fromarray(image)
    image.show()
image = Image.open('1.png')
#之后都会在np_img上进行运算
np_img = np.array(image)

使用的原图如下：

1 什么是图像增强

图像增强从大的方面上说就是，把这张图处理的更适合人看，但是从专业角度上说，有些比如去掉噪声、去掉运动模糊等虽然也是在改善视觉效果，但不叫图像增强。

2 基本运算

点运算：每个像素点都是独立的，直接计算；
领域运算：每个像素点和其周围的一个区域内的值是有关系的，比如根据周围点的值确定要计算的这个点的值，经常用的卷积运算就是属于领域运算。

点运算

# 点运算
def cal_point(image):
    np_img = image.copy()
    w, h = np_img.shape[0:2]
    for i in range(w):
        for j in range(h):
            np_img[i,j,:]  =  -np_img[i,j,:]+255
    return np_img

领域运算

# 领域运算
'''
每个加20再减去右边的像素值
'''
def cal_area(image):
    np_img = image.copy()
    w, h = np_img.shape[0:2]
    for i in range(w):
        for j in range(h):
            np_img[i,j,:] = np_img[i,j,:]+20
            if i != w-1:
                np_img[i,j,:] = np_img[i,j,:]-np_img[i+1,j,:]
    return np_img

先对图像进行领域运算之后再进行点的运算，结果如下。

3 线性拉伸

3.1 灰度拉伸

这部分为了实验效好，实验对象为下图

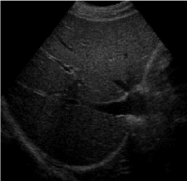
可以看到这张图中的亮度和对比度都比较低

这里正好介绍一下亮度和对比度，亮度就是所有像素值的平均值，对比度就是所有像素值的标准差

def linear_stretch(image):
    h, w = image.shape[0:2]
    np_image = image.copy()
    return np_image*2

将图像每个像素点都乘2，之后可以看到明显凉了一些，对比度也高了一点

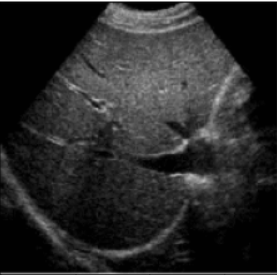
接着再把每个像素加上50个单位，结果如下：

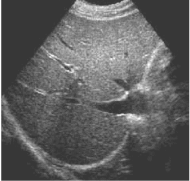
其中，我的理解就是，只是进行点运算，没干其他的事，每个点都是相对独立进行运算的，所以f(x, y)=f(x)+f(y)，以及f(cx)=cf(x)。
上面的变换也能简单写成
G = k*g + b，其中k>1的时候方差变大，相反就变小
一般我们希望让图像的最小值为0，最大值为255，那就确定出来两个点(gmin, 0), (gmax, 255)这样一来，就可以在变换的过程中确定比较合适的k和b。

3.2 均值方差规定化

常用的拉伸方法有两种，一种是上面的对灰度范围进行拉伸，但有些确定就是如果图像里有噪声，拉伸效果就不好，如果这个噪声点恰巧为0/255，那我们算最合适的k，b也就没什么效果了。
图像的性质有很多，除了上面的那些，还有一些比如平均值，方差以及标准差等。
那么就可以用平均值和标准差进行线性拉伸。假设原始图像均值b1, 对比度c1, 结果图像均值b2, 对比度c2，变换公式如下所示：

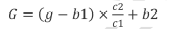
也是很好理解的

4 直方图及相关运算

就是把每个像素值有多少个点，统计出来，可以看出来分布的情况

def cal_histogram(image):
    gray_image = image[:,:,2]
    h, w = gray_image.shape[0:2]
    img = gray_image.copy()
    histogram = [0]*256
    for i in range(h):
        for j in range(w):
            histogram[img[i][j]] += 1
    return histogram

先统计第3节中原始图像的像素直方图情况，如下所示：

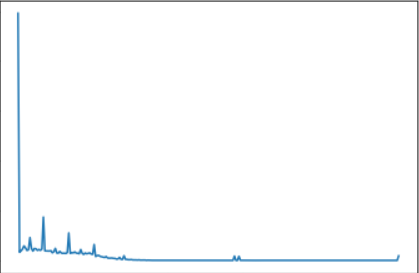
对于直方图均衡化操作
在信息论中，一个信息源带有的信息量H叫做熵，它与信源发出消息的概率相关(一些交叉熵，KL散度的问题，可以参照之前DLDL论文中的知识)，例如一张白纸蕴含的信息量就很少，如果一张图中各个灰度值等概率分布，所含的信息量就很大。
经过均衡化之后的对比图如下所示

4 对数变换

对数变换可以根据需要对某个像素区间的灰度值范围进行压缩，剩下的进行扩大，可以直接从对数函数的图像上看

可以看出，在比较小的部分，自变量变化一定的量，纵轴变化较大，到后来自变量变化相同的值，纵轴变化很小，也就实现了对图像的对数变换

# 对数变换
def log_transfer(image):
    gray_image = image[:,:,2]
    h, w = gray_image.shape[0:2]
    img = gray_image.copy()
    histogram = [0]*256
    for i in range(h):
        for j in range(w):
            if img[i,j]==0:continue
            img[i,j] = math.log(img[i, j])
    return img

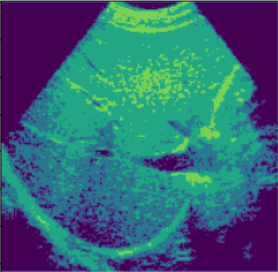
5 分块处理

如果有些图像经过一些手段，如均衡化等无效的话，可以对图像进行分块处理，在处理的过程中可能会出现块之间的分界线，这时可以将一个像素看作一个块，把这个像素周围的像素看作自己区域内的值，来计算均值和方差等值。