从数学本质出发,生成模型本质上是一种概率模型。它的生成过程可以表达成为数学中的两个过程,计算样本的概率分布和从概率分布中采样。
以最基本的无条件图像生成模型为例,我们需要构建出一个概率分布函数P(x),x为图像样本。它在x的像素空间中计算分布。在训练过程中,我们将x分为正负样本,正样本为现实世界中真实出现,有意义的图片。负样本为噪声图,没有意义的图片。在该种范式下,P(x)类似于判别器,需要将输入的x分类为好的图片和不好的图片,以此来计算x的无条件概率分布。
有了x的概率分布,我们接下来就需要在该概率空间中采样。采样得到的结果即是无条件生成的结果。对于难以直接采样的复杂概率分布,一般有接受拒绝采样和重要性采样的采样方法。简单来说,我们首先需要从常见概率分布比如正态分布中采出一定数量的样本,然后再筛去一部分原样本,使得剩下样本符合该复杂概率分布的分布。
但事实证明,我们无法使用上述方法进行生成。为了了解原因,我们首先需要对真实样本的分布进行一定的数学分析,我们将从黎曼几何的视角来观察真实世界的样本分布。
从几何视角观察,真实数据样本在高维空间中分布在一个低维流形表面。该流形在高维空间中连续且稀疏。因此在该空间均匀采样时,我们几乎不可能直接采样到流形表面上的点,需要花费高额不可承受的计算量才能生成一个样本。并且,我们难以引入条件进行条件控制生成。
在早期的生成模型中,为了加速采样过程,大多采用了重采样等手段。最常见的是AE-AD方法,使用神经网络编码器将高维数据压缩到一个很小的维度空间里,取得低维隐空间向量z,再使用解码器将低维向量映射回原空间中。但该方法大多只能应用于数据压缩,难以面对真正的生成任务,主要原因是我们依旧难以对z分布进行建模,而使用常见分布采样z大多生成的只是噪音数据。
对抗生成网络和变分自编码器在该问题上取得了突破。前者去掉了编码的过程,并将重采样应用于解码过程中。后者直接强制将数据编码为正态分布。在对抗生成网络中,由于难以在P(x)中采样,因此我们将其转化成为在P(x|z)的后验分布中进行采样。具体步骤先从正态分布中采样出z,然后通过神经网络重采样出x。由于难以计算P(x|z)后验分布,对抗生成网络直接粗暴的再引入一个判别器拟合该分布,最后将问题转化为了如何同时优化生成器和判别器。但因此也造成了训练收敛困难。变分自编码器在编码过程中将P(x)分布转化为Q(z),并在目标函数中保持Q(z)符合正态分布,并拥有随机噪声(方差)。但由于强行将复杂分布变化为简单分布,因此也造成变分生成器生成图像质量不佳,难以控制等问题。
现在我们换一个视角审视来这个问题。在难以获得P(x)分布函数的情况下,我们可以使用蒙特卡洛-马尔可夫采样法。该方法将采样过程视作为一个随机过程,每个新样本只和旧样本有关P(xn|xn-1,xn-2,....,x0)=P(xn|xn-1)。我们可以将该采样视作为一个SDE,而我们只需要使用神经网络来拟合SDE即可完成完整的采样。
我们可以从物理学中分子动力学的角度来更加直观的诠释这个过程。我们将分布看作是物理模型中的势能场,样本看作是模型中的粒子。初始状态下所有粒子在物理场中均匀分布。在每个时间步中,每个粒子都趋向往具有更低势能的方向运动,但同时也可能收到其他粒子运动的干扰。经过一段时间步后,粒子分布趋于稳态,粒子分布密度与场分布基本一致。这时随机取出n个粒子,这些粒子的分布就是我们要的最终目标。
因此我们也可以使用朗之万动力学和伊藤扩散来诠释这个问题。这个物理模型可以很好的通过SDE过程来计算分子在势能场中的运动。
mdv/dt = -γv + F + ξ(t)
- m:粒子的质量,通常是一个常数。
- v:粒子的速度,是随时间变化的量。
- t:时间,是独立变量。
- γ:粘滞阻力系数,是一个描述介质阻力大小的常数。
- F:外力,是一个随时间变化的量,可以是一个恒定的力或者一个随机力。
- ξ(t):随机力,是一个随时间变化的随机量,用来描述粒子受到的介质分子热运动的影响。
现在我们只需要得到F,即可推导出扩散的SDE过程。我们可以使用ΔP(x)来表达样本所受到的外力。从数学角度看,ΔP(x)表示每一步SDE的得分,该方法即是score matching。
现在让我们观察P(x)。我们将P(x)更换一种写法。令:

其中, E(x)<= 0,Z为归一化因子。我们对上式两边取对数求导,得到:
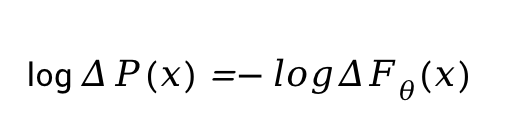
这样,我们就不需要计算归一化因子,转而去专心表达样本所在的能量场。为了保证F(x)在其定义域内恒大于0,我们使用下式表达F(x)。
其中E(x)被称作能量模型,其对应上文所提到的势能场。从能量模型转化的概率分布模型即是玻尔兹曼分布。现在我们只需要使用神经网络计算E(x),使真实数据出现的位置势能尽可能低即可。
这时候,我们已经获得了基础扩散模型的推断和目标函数。上式即为denoising diffusion probabilistic models论文中的L-simple函数。
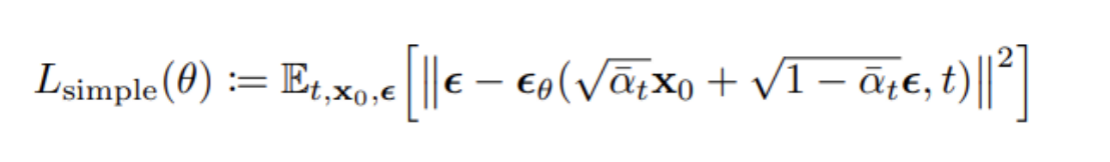
我们还面临着最后一个主要问题。在上文中所提,真实数据分布于高维空间的低维流形表面上,大部分位置概率密度都无限接近于0。大部分样本都初始化于稀疏空间中,当梯度为0时,我们无法在有限的迭代步骤中得到目标。解决该问题的方法是给样本加入高斯噪声。由于高斯噪声作用于整个样本空间。因此我们可以从空间中任何一个点取得梯度,并在有限迭代步中取得平稳样本。该步骤即是denoising diffusion probabilistic models训练方法中的前向加噪步骤。
最后,依据上述理论,完整的训练过程表达如下:

上述的扩散模型都是基于像素级别的扩散。其中X0是原图像,Zt是t时刻的噪声,X1~Xn都是关于X0的隐向量。像素级别扩散的主要问题是难以有效生成清晰图像,通常需要再额外训练超分辨率模型。现在重新观察扩散模型的生成步骤。我们发现,由于X1~Xn都是X0的隐空间样本,那么我们可以将X0先压缩到维度更小的隐空间,最后再从隐空间转换回来。在stable diffusion中,我们首先使用预训练的VAE模型将512x512x3尺寸的张量将样本压缩进64x64x4的隐空间,然后对隐空间进行加噪去噪,最后再用AD还原回样本,完成生成过程。
我们还有最后一个主要问题,如何实现条件引导生成。在上述推导中不难发现,我们很难直接表达P(x|c)的后验分布(c为条件)。因此,我们使用贝叶斯公式将P(x|c)转化为似然和先验概率,加入log简化计算:
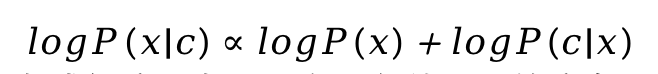
其中,上式左项为无条件生成部分,右项为在x条件下c的分布。不难看出,我们可以额外训练一个判别器来取代右侧部分。这即是classifier guidance的条件控制方法,被Imagen模型采用。在去噪的过程中,我们只需要在每一步额外计算判别器的梯度即可实现有条件生成。这种方法训练成本较低,实现较为简单。但面临与GNN方法类似的问题,一是判别器和生成器在其中产生对抗效果,二是生成器可能会寻找欺骗判别器的方法。
我们现在不想引入额外的部分使生成模型变得更为复杂,我们需要寻找一种classifier-free guidance的方法。我们将上式右项再次贝叶斯,得到:
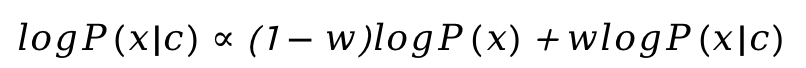
其中w为condition scale。我们现在只需要分别训练无条件生成器和有条件生成器即可引导有条件的生成模型。该方法避开了加入判别器的缺陷,但面临了训练成本高的问题。但训练完成效果远好于classifier guidance的方法,因为它不再依赖于判别器性能。其是现在最主流的生成器模型,被Dalle2,Stable Diffusion广泛采用。
现在我们重点分析Stable Diffusion的模型结构:
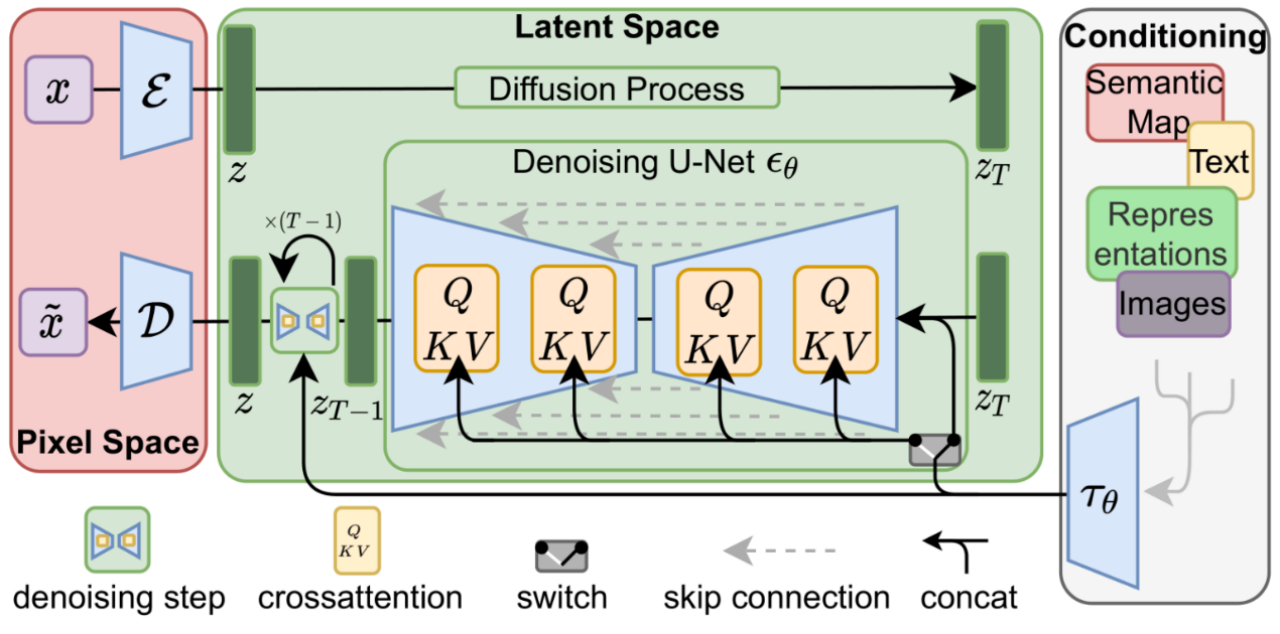
在左侧部分,模型使用变分自编码器-解码器将样本从像素空间转化进隐空间,加噪得到噪声样本。Denoising U-Net计算每一步分数,即噪声。Unet结构保证每一步去噪神经网络不会忽略任何信息,其由attention结构和残差结构交替连接,并使用卷积层进行上采样和下采样。Cross attention使用于条件引导控制。文本引导的token embeddings由预训练的clip模型生成。


