Survival Analysis

上一个工作结束之后，最近开始了一个新课题，Survival Analysis，本篇博客将主要介绍生存分析中的一些基本概念和方法的分类

1 基本概念

生存分析顾名思义就是对于生存状态的分析，它其实是一个比较宽泛的概念，并不一定是人的生存状态，例如一个公司的发展以及工业上一个零件的使用寿命等都可以进行生存分析。生存分析的目标就是根据输入以及相关的影响因素推测目标在时间点t时的生存状态。

这里给出一些标识符号的说明，以便后文的描述。

2 Censoring

在实际的生存分析中，数据的收集周期不可能是无限长的，对于采样对象的观察也存在很多不确定因素，因此数据很容易出现提前结束或者记录的生存时间并不是真实的，只能代表在这个时间之前对象还在生存，这个现象被称为截断（censored）。截断分为以下几种，

right-censoring：右截断，也就是采样对象提前结束，代表时间t之前对象生存；
interval censoring：阶段阶段，没有确定的截断时间，只给出一个模糊的范围；
left-censoring：左截断，开始截断有一部分截断数据

出现比较多的是第一种rc，主要对其进行研究，后文方便起见，截断就是指右截断。举一个例子更清楚看一下什么是右截断。

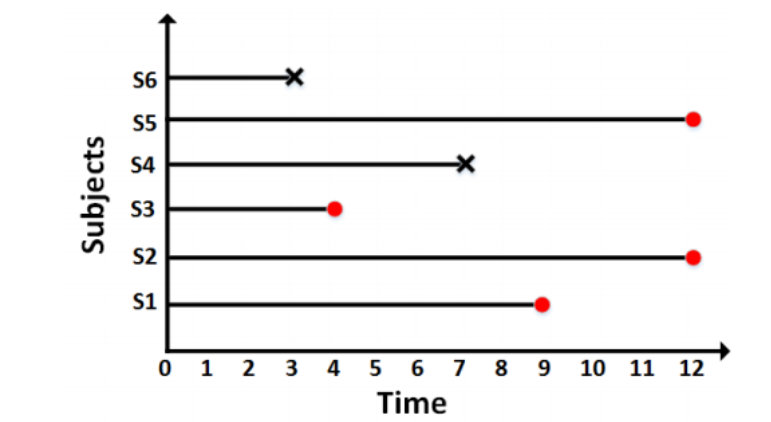
红色的点代表截断数据，横轴代表月份，观测时间12个月。4月和9月的数据表示在观测时间之前就退出，后两个有几个可能，第一个是12月份正好退出，第二个是12月份没发生事件但是也没观测到时间。

在输入数据中，如果instance未发生截断，时间的标签就是生存时间，如果发生截断，时间的标签就是发生截断的时间。

3 几个重要function

生存分析中还有几个比较重要的概念，分别是survival function以及cumulative death distribution function

首先survival function表示的是时间节点t之前，未发生时间的可能性，很显然这应该是一个单调递减的函数，因为在开始即t=0的时刻，生存率是1。具体公式表示如下：

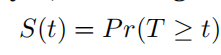
cumulative death distribution function是和它相反的概念，代表时间t之前就发生时间的概率，也就是F(t)=1-S(t)

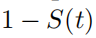
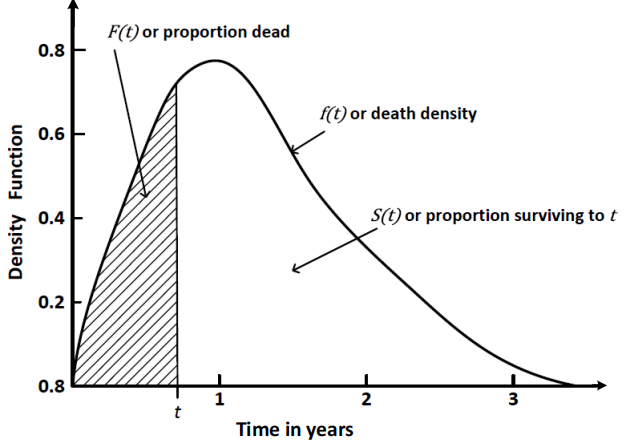
F的概率密度函数也很容易得到，这三个表示的关系如下：

另外在生存分析中很多方法不直接对生存时间进行分析，而是回归出一个hazard值，用这个作为待回归的目标进行分析，这里介绍hazard function。

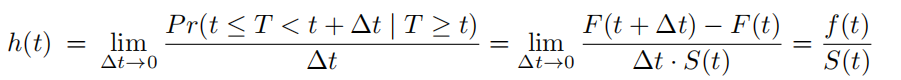
直接放公式吧，看完公式应该很好理解，它并不是为了预测时间t的生存概率，而是为了表示时间t之前事件未发生的概率。在这个领域比较著名的cox based方法大多预测hazard。

4 Taxonomy

生存分析的方法大致分为两类，基于统计和基于机器学习。先将分类列举如下：

基于统计
- Non-parametric: Kaplan-Meier
- Semi-parametric: Cox Regression，这里除了basic的cox之外常用的是Regularized Cox例如传统的Lasso Cox，Ridge Cox等
- Parametric： Linear Regression，这里也有很多变种比如Buckley-James或者To bit或者加有惩罚项的

基于机器学习

Survival Trees
Bayes
Neural Networks
SVM
最近火一些的Active Learning，Ensemble fusion，Transfer Learning以及Multi-task和Meta-learning的

当然还有一些方法可以作为生存分析的pre-processing，例如数据的calibration或者将数据统一转化为pseudo value，再进行学习，以消除机器学习模型在截断和非截断数据上学到的分布存在shift。

这次的博客其实就结束了，这方面的论文可能不太好找，这里贴两篇最近看的文章，还有自己的一些总结，感兴趣的可以通过这两篇文章找到更多相关领域的工作。有问题也欢迎留言讨论。

ID	Paper title	Authors	Publiction	Hightlights
1	DeepHit: A Deep Learning Approach to Survival Analysis with Competing Risks	Changhee Lee，William Zame，Jinsung Yoon，Mihaela van der Schaar	AAAI 2018	常用的cox based model一方面对coefficient和其他变量之间有很强的约束(比如假设是线性约束等)，另一方面不显示的预测时间。本文提出的DeepHit，将生存时间转化为离散的值，回归转化为分类，直接预测生存时间。对于censored数据，提出对应损失函数解决，思想主要是，我们至少可以知道发生censored之前该病人是没有死亡的，将一个很确定的时间及发生一定发生的概率进行转换。另外可以同时分析多个死亡原因（不再只是针对一个疾病的0/1可以是0/1/2等）
2	T-SCI: A Two-Stage Conformal Inference Algorithm with Guaranteed Coverage for Cox-MLP	Jiaye Teng, Zeren Tan, Yang Yuan	ICML 2021	cox regression假设coefficient和结果之间是线性关系，所以一定程度上缓解censored数据影响，但是cox约束太强。后来神经网络的方法放松了假设，在censored和uncensored上学的分布就会有偏移。和以往在神经网络基础上解决censored数据影响的方法不同，本文基于cox based model进行(即不显示预测时间)。引入加权的保角推理构造新的loss进行回归。