Label Distribution Learning 论文阅读
近两个月读了很多论文,但是我读的目的大多是为了了解一个方向,也没有动手实验,读了之后印象不是很深。我觉得不太行,这样效率有点低,所以计划从2021.2月每周读懂2-3篇高质量论文,总结1-2篇博客,开源代码的仔细学习一下内容和编码风格,没有开源的自己尝试编写。目前也已经筛选出来了自己感兴趣或者自己必须要读的7篇论文,先这样一个月开开效果咯。
这篇论文是和自己毕设相关,如题目,主要是介绍一个LDL的算法,对我来说是一个比较新的东西,不过这篇文章介绍的很详细,在这里总结一下,开启一波阅读论文的计划。
1、什么是Label Distribution Learning (LDL)
看到distribution,应该会想到这是一个关于Label的分布情况,我们常说的distribution主要是概率分布,这时脑海里能浮现出来一副曲线图,这里的LDL其实就是给一个图片的标签分配不同的degree,这些degree都在[0, 1]之间,而且和为1。先放一张LDL中label的示例图吧,如图1。
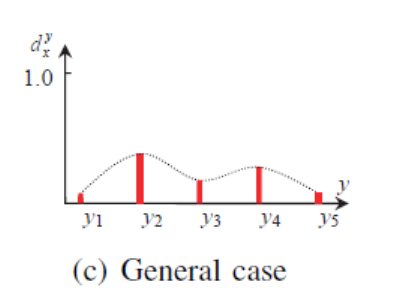
图 1
那么这些degree有什么意义呢?
不同degree代表着它对实例x的描述度不同,通俗点讲就是degree越高代表着它越能代表这个实例。比如说在一副图片中有很多物体,有船有海水有太阳有海鸥....那么,如果问你这是什么图片,你可能会说是船的图片,也可能会说是海水的图片,但很少会直接说这是一张太阳或者海鸥的图片,这其实和人视觉中自身的注意力有关,越大越醒目的目标会越早的被发现。另一方面也是说,船和海水更能描述或者代表这幅图片。因此,船和海水的degree就相对于海鸥和太阳要高一些。
重点来了,上面说了这么多,LDL到底是什么呢?其实很简单,LDL就是对与Label Distribution的学习呀,也就是对每个标签degree的学习。
2、Label Distribution Learning (LDL)要干什么
LDL是干什么的其实很简单,就是用来学习Label Distribution的,最后就是要学出来每个标签的description degree。
3、LDL和Single Label Learning ( SLL)以及Multi Label Learning(MLL)的区别
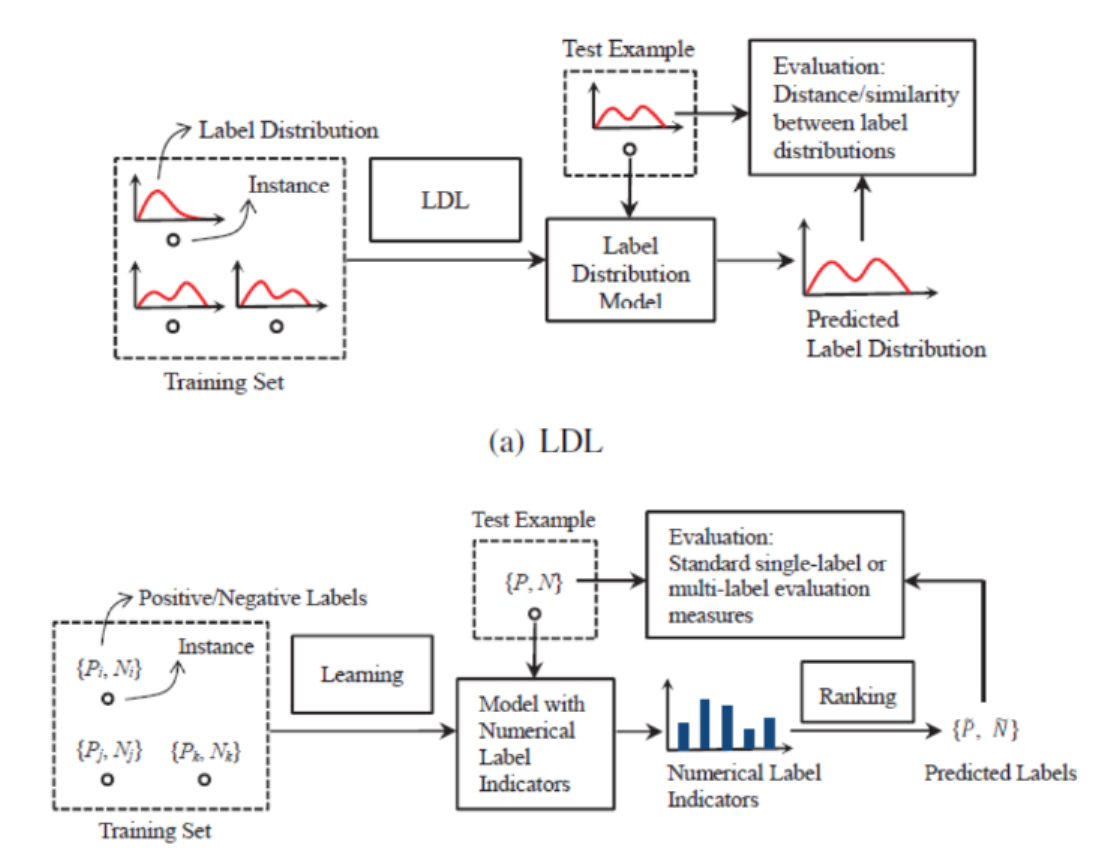
主要区别如下:
- LDL的标签是从数据中来的,并不像常见的任务,label是人定义的,比如说one-hot编码等。这样到底有什么好处我还没验证过,但是我觉得对于数据来说,肯定会保留到更多的信息,不会破坏原有的分布等;
- LDL最后是关注标签的一个分布,然而其他的任务只在乎你是0还是1;
- 所用的评价方法不同;
- 最后这个严格意义上不能算是区别,就是LDL中出现的Label都是positive的,只是说对于实例的描述程度有所区别而已,这个和一些问题还是有区别的,并不是说我设定一个threshold,最后预测出来有很多,但是大于这个threshold的才是positive。
MLL和SLL其实都是LDL的一个特例而已,首先对于MLL,就是每个label所分配的degree是相同的(这只是最原始的做法,目前很多方法都已经开始关注标签之间的dependency),对于SLL就是每个instance只有一个label,而且label的degree是1,从另一方面将LDL其实比MLL和SLL都要更加的灵活。除了灵活之外,LDL还有更大的输出空间,比如共有C个标签,对于一个实例X来说,单标签分类中有C个可能的输出,多标签分类中有2^C-1个输出,但是LDL其实就是把MLL和degree的取值放在了一起,是无限可能性的。
4、Label Distribution Learning Algorithm
标签分布学习有三种方式,将LDL问题转化为SLL问题或者MLL问题、使用现有的方法进行改进以及为LDL问题设计特定的算法
1)transform to existing algorithm
例如一个实例X的标签为(Xi, Di),其中Di是一系列描述度d。那么将其转化为SLL问题就是根据degree(weight),将其转化到(Xi, Yi)上就可以,剩下的就是和正常的SLL或者MLL是一样的
2)existing algorithm adapt
首先可以使用KNN(作为一种简单到应用十分广泛的分类方法,这里要区别于无监督聚类的K-Means),首先就是找N个相邻的点,然后根据邻近K个点在Yi处的degree的平均值来赋值给这个实例在Yi初的degree,这样将所有的degree都求出来之后,就最后得到了分布。
另一种方法可以使用NN,其实就是C个output unit,然后对每个进行Softmax缩到0-1之间,且和为1,就可以了!
3)special algorithm
这里介绍了俩算法,有一个数学要求高一点还没看懂,之后继续看一下
这个算法叫做SA-IIS。首先这里使用的评估方式KL散度,也就是相对熵,是为了评估两个模型之间的差异,注意哦,是两个模型,也就是说目标的熵是会变化的。那这时候可能会问,之前的分类任务中多使用交叉熵,和这个相对熵有什么区别呢?之后请看插播内容5!
首先用KL散度的方式写出目标函数:
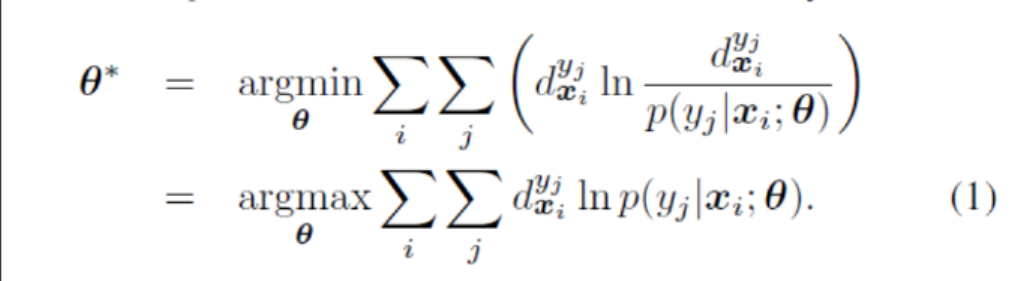
之后在SA-IIS算法中假设模型是一个最大熵模型,所以评估出来的参数模型值:
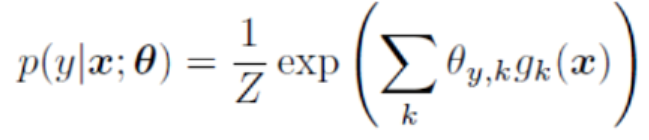
往里面代!
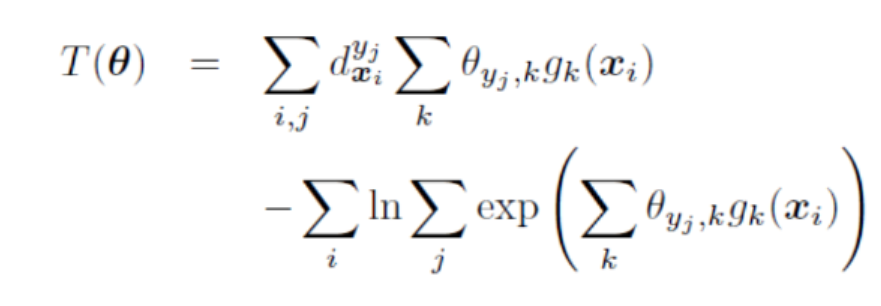
所以就是求每个时间布的差值,然后不断让这个差值缩小就可以啦
算法的伪代码如下所示:

好了结束!
5、信息量、熵、相对熵,交叉熵
这部分确实是知识空白啊,还是需要仔细补一下的,在那之前先全面了解一下
信息量:每个东西自身都包含的有信息量,比如我是一个男的,这个信息的不确定性就很小,所以信息量很少,我们经常说的信息量很大有时候都是那种听完之后令我们很震惊的事情,这里的信息量也是,不确定性越大越不能理解,信息量就越大
熵:有了一个东西的信息量之后,把这个事物所有发展可能性的期望算出来,就是熵
相对熵:有了熵,相对熵就是很好理解的概念,就是相对的嘛,这里列举一个P和Q,分别是真实的分布和预测的分布,log(P/Q),这个就能评估Q接近P的程度或者说Q对P的拟合程度,越接近越小,所以相对熵越小,Q的效果就越好
交叉熵:之前的都没有放公式,因为都要截图看起来很乱,但这里不放不行了
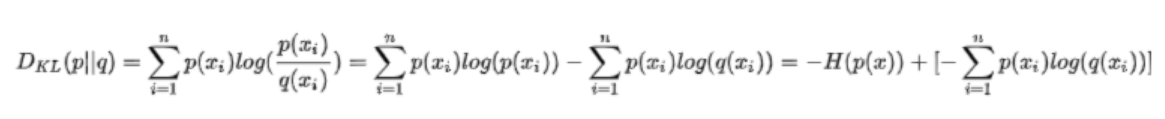
左侧是相对熵也就是KL散度,也叫KL距离(但这里的距离不是真距离,不具备对称性),之后就是将公式变形呗,可以发现其实是熵+一个部分组成,这个部分就是交叉熵。先了解到这里,回答一下之前的问题,为什么在多分类任务当中,使用交叉熵呢?因为标签是0,1这样的确定值,所以熵呢就是一个确定的值,所以就可以用交叉熵来评估,那为什么在交叉熵和KL都可以的情况下用交叉熵呢?我猜,运算简单?


