Mutual Information Neural Estimation

在读完Prof. Tishby的利用 information bottleneck 来解释深度学习的文章，“Opening the black box of Deep Neural Networks via Information” 之后，利用互信息做了一些尝试，出现了一些无法理解的现象。所以近期又对Mutual Information相关的文章进行了学习。

1. 介绍

Mutual Information(MI)互信息在深度学习领域的应用日益广泛，但还是存在一些问题，其中最关键的就是MI的计算很困难，很多工作都是尝试通过找到MI的界来求MI，本次介绍的文章是ICML2018使用一个神经网络作为MI estimator的工作，思路清晰，实验以及理论证明充分。

2. 方法细节

本节将介绍MI相关的知识以及如何获得一个MI的下界。

2.1. Mutual Information

互信息 $I$ 可以表示两个变量 $X$ 和 $Z$ 之间的依赖程度，$I$ 越大，表示两个随机变量的依赖程度越大。$I(X;Z)$ 可以表示为：
$I(X;Z) = H(X)-H(X|Z) = H(Z)-H(Z|X) = I(Z;X)$
这里的H表示信息熵，计算方式是 $H(X) = -E_p(x)logp(x)$，另外H(X|Z)代表条件熵，计算方式为 $H(X|Z)=-E_p(x,z)logp(x|z)$。条件熵得到的具体过程这里不再展开，需要的可以看一下西瓜书有关信息熵的部分。
对于互信息，其实可以对其计算方式进行转化，过程如下：
$I(X;Z)$ = $H(X)$−$H(X|Z)$
=−$\int_xp(x)logp(x)dx +$ $\int_xp(x,z)logp(x|z)dxdz$
=$D(P(X,Z)||P(X)P(Z))$
所以互信息可以看作联合分布和两个边际分布乘积的KL散度。如果两个随机变量完全一致，MI就为0。

2.2. The Donsker-Varadhan Representation of KL

尽管上文中已经得到了如何通过KL散度计算得到互信息，但是这里的KL散度其实也是无法计算得到的。我们现在一起考虑一个普通的Encoder model，我们就只有 $P(Z|X)$。然而$P(X,Z)$,$P(X)$,$P(Z)$都是无法得到的。因此我们需要找到一个可以计算得到的目标表示来进行优化，这里我们使用Donsker-Varadhan(DV) representation：
$DKL(P||Q)=supE_p[T]-log(E_Q[e^T])$
其中$P$和$Q$是两个独立分布，$T$是一个映射函数。
证明过程公式比较多，但还是很有必要放一下的，所以就贴图吧（开始偷懒
我们想要证明上面的式子，就是要证明：

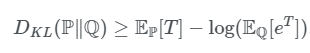
在一些$T$符合条件的时候，上式成立。
首先我们定义一个分布$dG = 1/ze^TdQ$。换一种方式，这个分布可以表示为$g(x)=1/ze^T(x)q(x)$。为了保证这个$g(x)$是一个概率密度函数，我们需要对其中的项进行一个定义。
有了上面的定义之后，我们就可以把不等式右边的式子转化为如下：

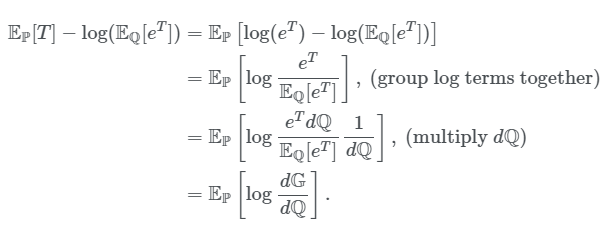
我们使得$\Delta$等于如下：

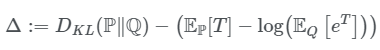
接着可以用KL散度的形式对上式进行转化：

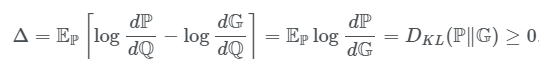
这样定义之后，我们要证明的不等式就在任何时候都成立了。

2.3. The f-Divergence Representation of KL

使用f-Divergence Representation of KL可以得到一个稍微弱一些的界。

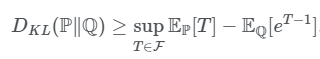
这个界相对较弱，主要是因为$E_Q[e^T-1]>log(E_Q[e^T])$。这个比较好得到，因为存在一个不等式$x/e>logx$。

2.4. Mutual Information with DV

在上面的式子中，MI被表示为和KL散度相关的形式，$D(P(X,Z)||P(X)P(Z))$。我们有了DV推出来的MI的界，如下：

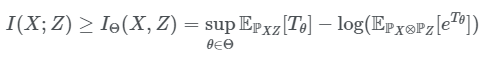
在这个式子里面，我们可以使用$X$和$Z$的采样得到分布，以此来得到上式中的界，剩下的不好计算的概率值就直接可以不计算了，而且这个界是收的比较紧的。

2.5. Mutual Information Neural Estimator

终于，要介绍本篇论文的MINE。
使用一个神经网络$T$和$n$个属于$X$的样本，我们就可以得到如下计算MI的式子：

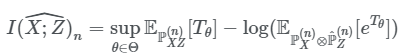
其中出现的分布都是经验分布，一个比较好理解的例子就是，这里的$X,Z$就是我们想比较MI的两个分布。MINE具体的优化过程这里也不放了，图多了会有些乱，直接看paper吧。
最后根据数据得到的$T$的梯度如下：

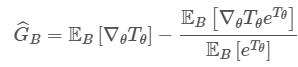
这里的$B$是数据的batch。

2.6. Bias in Gradient

到这里其实已经解决了最主要的问题，即如何求MI。但现在还有一点瑕疵就是我们这里采样估计的时候用的都是batch，那么2.5节最后估计出来的gradient就是有bias的。所以这里直接可以用滑动平均来缓解这个问题。

3. 对自己遇到的问题的思考

3.1. Problem

使用Mutual information来看一下自己的改进有没有用，具体的说就是加完自己设计的模块之后，MI的表现，在$I(Y;T)$上有没有表现得更好一些。困扰我很久的问题就是，就算方法的点数高了不少，但MI就是没有变化，很迷:)

3.2. Conclusion

目前的结论是这样的，Prof. Tishby论文中主要在几层MLP上看实验结果，而且数据相当于是toy data。换到conv上之后就出现了一些问题，一些网友也尝试直接把论文中统计MI的方法迁移到含有conv的模型中，也和我遇到了一样的问题，中间涉及到了映射稀疏的问题，导致一些现象没有变化。
所以，想要将MI推广到普遍的模型中去，还是要找到一个通用的MI estimator才可以。后来搜论文的时候，碰巧看到了这篇MINE，感觉可以解决我的问题，如果结果还可以的话，会再更新一篇文章对出现这个现象的原因做一个更加深入具体的分析。